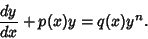 |
(1) |
Let
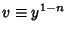 for
for 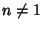 , then
, then
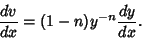 |
(2) |
Rewriting (1) gives
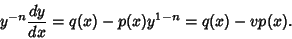 |
(3) |
Plugging (3) into (2),
![\begin{displaymath}
{dv\over dx} = (1-n)[q(x)-vp(x)].
\end{displaymath}](b_455.gif) |
(4) |
Now, this is a linear First-Order Ordinary Differential Equation
of the form
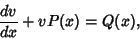 |
(5) |
where
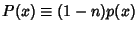 and
and
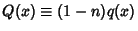 . It can therefore be solved analytically using an
Integrating Factor
. It can therefore be solved analytically using an
Integrating Factor
where 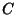 is a constant of integration. If
is a constant of integration. If 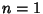 , then equation (1) becomes
, then equation (1) becomes
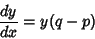 |
(7) |
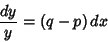 |
(8) |
![\begin{displaymath}
y=C_2 e^{\int [q(x)-p(x)]\,dx}.
\end{displaymath}](b_464.gif) |
(9) |
The general solution is then, with 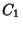 and
and 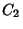 constants,
constants,
![\begin{displaymath}
y = \cases{
\left[{{{(1-n)\int e^{(1-n)\int p(x)\,dx} q(x)\...
...or $n\not=1$\cr
C_2 e^{\int [q(x)-p(x)]\,dx} & for $n=1$.\cr}
\end{displaymath}](b_465.gif) |
(10) |
© 1996-9 Eric W. Weisstein
1999-05-26
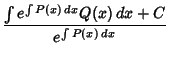
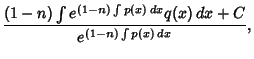
![\begin{displaymath}
y = \cases{
\left[{{{(1-n)\int e^{(1-n)\int p(x)\,dx} q(x)\...
...or $n\not=1$\cr
C_2 e^{\int [q(x)-p(x)]\,dx} & for $n=1$.\cr}
\end{displaymath}](b_465.gif)