A procedure for finding the quadratic factors for the Complex Conjugate Roots of a
Polynomial 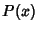 with Real Coefficients.
with Real Coefficients.
![\begin{displaymath}[x-(a+ib)][x-(a-ib)] = x^2+2ax+(a^2+b^2) \equiv x^2+Bx+C.
\end{displaymath}](b_76.gif) |
(1) |
Now write the original Polynomial as
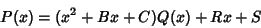 |
(2) |
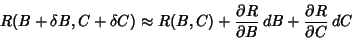 |
(3) |
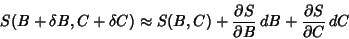 |
(4) |
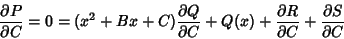 |
(5) |
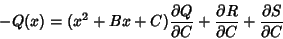 |
(6) |
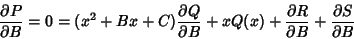 |
(7) |
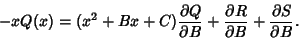 |
(8) |
Now use the 2-D Newton's Method to find the simultaneous solutions.
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in C: The Art of Scientific
Computing. Cambridge, England: Cambridge University Press, pp. 277 and 283-284, 1989.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() with Real Coefficients.
with Real Coefficients.