|
|
|
A generalization of Clebsch-Gordan Coefficients and Wigner 3j-Symbol which arises in the coupling of three angular momenta. Let tensor operators ![]() and
and ![]() act, respectively, on subsystems 1 and 2 of a system, with subsystem 1 characterized by angular momentum
act, respectively, on subsystems 1 and 2 of a system, with subsystem 1 characterized by angular momentum ![]() and
subsystem 2 by the angular momentum
and
subsystem 2 by the angular momentum ![]() . Then the matrix elements of the scalar product of these two tensor
operators in the coupled basis
. Then the matrix elements of the scalar product of these two tensor
operators in the coupled basis
![]() are given by
are given by
|
|
|
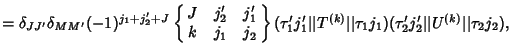
|
(1) |
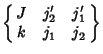 is the Wigner
is the Wigner
Edmonds (1968) gives analytic forms of the ![]() -symbol for simple cases, and Shore and Menzel (1968) and Gordy and Cook (1984) give
-symbol for simple cases, and Shore and Menzel (1968) and Gordy and Cook (1984) give
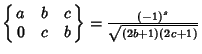
|
(2) |
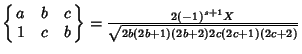
|
(3) |
![$\left\{\matrix{a & b & c\cr 2 & c & b\cr}\right\}={2(-1)^s[3X(X-1)-4b(b+1)c(c+1)]\over\sqrt{(2b-1)2b(2b+1)(2b+2)(2b+3)(2c-1)2c(2c+1)(2c+2)(2c+3)}},\quad$](w_946.gif)
|
(4) |
| (5) | |||
| (6) |
See also Clebsch-Gordan Coefficient, Racah V-Coefficient, Racah W-Coefficient, Wigner 3j-Symbol, Wigner 9j-Symbol
References
Carter, J. S.; Flath, D. E.; and Saito, M. The Classical and Quantum
Edmonds, A. R. Angular Momentum in Quantum Mechanics, 2nd ed., rev. printing.
Princeton, NJ: Princeton University Press, 1968.
Gordy, W. and Cook, R. L. Microwave Molecular Spectra, 3rd ed. New York: Wiley, pp. 807-809, 1984.
Messiah, A. ``Racah Coefficients and `
Rotenberg, M.; Bivens, R.; Metropolis, N.; and Wooten, J. K. The
Shore, B. W. and Menzel, D. H. Principles of Atomic Spectra. New York: Wiley, pp. 279-284, 1968.
![]() -Symbols. Princeton, NJ:
Princeton University Press, 1995.
-Symbols. Princeton, NJ:
Princeton University Press, 1995.
![]() ' Symbols.'' Appendix C.II in Quantum Mechanics, Vol. 2.
Amsterdam, Netherlands: North-Holland, pp. 567-569 and 1061-1066, 1962.
' Symbols.'' Appendix C.II in Quantum Mechanics, Vol. 2.
Amsterdam, Netherlands: North-Holland, pp. 567-569 and 1061-1066, 1962.
![]() and
and ![]() Symbols. Cambridge, MA: MIT Press, 1959.
Symbols. Cambridge, MA: MIT Press, 1959.
|
|
|
© 1996-9 Eric W. Weisstein