Weyl Tensor

The Tensor

$${C^{ij}}_{kl} = {R^ij}_{kl} -2{\delta^{[i}{}_[k}{R^{j]}}{}_{... ...\textstyle{1\over 3}} {\delta^{[i}}{}_{[k}{\delta^{j]}}_{l]}R,$$

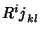where ${R^ij}_{kl}$ is the Riemann Tensor and 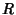$R$ is the Curvature Scalar. The Weyl tensor is defined so that every Contraction between indices gives 0. In particular, 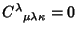${C^\lambda}_{\mu\lambda\kappa}=0$. The number of independent components for a Weyl tensor in 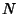$N$-D is given by

$$C_N = {\textstyle{1\over 12}} N(N+1)(N+2)(N-3).$$

See also Curvature Scalar, Riemann Tensor

References

Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, p. 146, 1972.