Let a Group 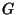 have a presentation
have a presentation
so that 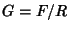 , where
, where 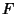 is the Free Group with basis
is the Free Group with basis
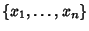 and
and 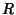 is the
Normal Subgroup generated by the
is the
Normal Subgroup generated by the 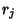 . If
. If 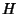 is a Group with
is a Group with
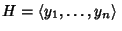 and if
and if
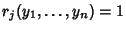 for all
for all 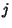 , then there is a surjective homomorphism
, then there is a surjective homomorphism 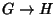 with
with
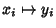 for
all
for
all 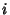 .
.
See also Free Group, Normal Subgroup
References
Rotman, J. J. An Introduction to the Theory of Groups, 4th ed. New York: Springer-Verlag, p. 346, 1995.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() have a presentation
have a presentation