|
|
|
A volume element is the differential element ![]() whose Volume Integral over some range in a given coordinate system gives the
Volume of a solid,
whose Volume Integral over some range in a given coordinate system gives the
Volume of a solid,
| (1) |
| (2) |
The use of the antisymmetric Wedge Product instead of the symmetric product
![]() is a technical
refinement often omitted in informal usage. Dropping the wedges, the volume element for Curvilinear Coordinates in
is a technical
refinement often omitted in informal usage. Dropping the wedges, the volume element for Curvilinear Coordinates in
![]() is given by
is given by
| (3) | |||
| (4) | |||
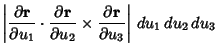 |
(5) | ||
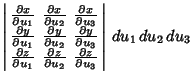 |
(6) | ||
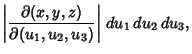 |
(7) |
See also Area Element, Jacobian, Line Element, Riemannian Metric, Scale Factor, Surface Integral, Volume Integral
References
Gray, A. ``Isometries of Surfaces.'' §13.2 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 255-258, 1993.