Given Vectors 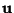 and
and 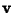 , the vector direct product is
, the vector direct product is
where 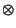 is the Matrix Direct Product and
is the Matrix Direct Product and
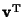 is the matrix Transpose. For
is the matrix Transpose. For 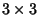 vectors
vectors
Note that if
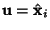 , then
, then
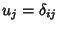 , where
, where 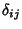 is the Kronecker Delta.
is the Kronecker Delta.
See also Matrix Direct Product, Sherman-Morrison Formula, Woodbury Formula
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() , the vector direct product is
, the vector direct product is
![\begin{displaymath}
{\bf u}{\bf v} = \left[{\matrix{u_1{\bf v}^{\rm T}\cr u_2{\b...
...v_1 & u_2v_2 & u_2v_3\cr u_3v_1 & u_3v_2 & u_3v_3\cr}}\right].
\end{displaymath}](v_450.gif)