Let ![$[\arg f(z)]$](v_297.gif) denote the change in argument of a function
denote the change in argument of a function 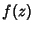 around a closed loop
around a closed loop 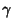 . Also let
. Also let 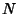 denote
the number of Roots of
denote
the number of Roots of 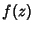 in
in 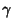 and
and 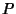 denote the number of Poles of
denote the number of Poles of 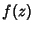 in
in
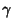 . Then
. Then
![\begin{displaymath}[\arg f(z)]= {1\over 2\pi}(N-P).
\end{displaymath}](v_300.gif) |
(1) |
To find ![$[\arg f(z)]$](v_297.gif) in a given region
in a given region 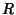 , break
, break 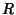 into paths and find
into paths and find ![$[\arg f(z)]$](v_297.gif) for each path. On a circular
Arc
for each path. On a circular
Arc
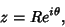 |
(2) |
let 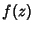 be a Polynomial
be a Polynomial 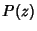 of degree
of degree 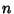 . Then
. Then
Plugging in
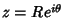 gives
gives
![\begin{displaymath}[\arg P(z)]= [\arg Re^{i\theta n}] + \left[{\arg { P(Re^{i\theta})\over Re^{i\theta n}}}\right]
\end{displaymath}](v_307.gif) |
(4) |
![\begin{displaymath}
\lim_{R\to \infty} {P(Re^{i\theta})\over Re^{i\theta n}} = \hbox{[constant]},
\end{displaymath}](v_308.gif) |
(5) |
so
![\begin{displaymath}
\left[{ P(Re^{i\theta})\over Re^{i\theta n}}\right]= 0,
\end{displaymath}](v_309.gif) |
(6) |
and
![\begin{displaymath}[\arg P(z)]= [\arg e^{i\theta n}] = n(\theta_2-\theta_1).
\end{displaymath}](v_310.gif) |
(7) |
For a Real segment 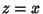 ,
,
![\begin{displaymath}[\arg f(x)]= \tan^{-1}\left[{0\over f(x)}\right]= 0.
\end{displaymath}](v_312.gif) |
(8) |
For an Imaginary segment 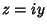 ,
,
![\begin{displaymath}[\arg f(iy)]= \left\{{\tan^{-1} {\Im[P(iy)]\over \Re[P(iy)]}}\right\}_{\theta_1}^{\theta_2}.
\end{displaymath}](v_314.gif) |
(9) |
Note that the Argument must change continuously, so ``jumps'' occur across inverse tangent asymptotes.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() denote the change in argument of a function
denote the change in argument of a function ![]() around a closed loop
around a closed loop ![]() . Also let
. Also let ![]() denote
the number of Roots of
denote
the number of Roots of ![]() in
in ![]() and
and ![]() denote the number of Poles of
denote the number of Poles of ![]() in
in
![]() . Then
. Then
![$\displaystyle \left[{\arg\left({z^n {P(z)\over z^n}}\right)}\right]$](v_304.gif)
![$\displaystyle [\arg z^n] + \left[{\arg \left({P(z)\over z^n}\right)}\right].$](v_305.gif)
![\begin{displaymath}[\arg f(iy)]= \left\{{\tan^{-1} {\Im[P(iy)]\over \Re[P(iy)]}}\right\}_{\theta_1}^{\theta_2}.
\end{displaymath}](v_314.gif)