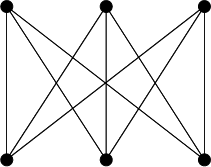
|
|
|
The utility problem asks, ``Can a Planar Graph be constructed from each of three nodes (`house owners') to each of
three other nodes (`wells')?'' The answer is no, and the proof can be effected using the Jordan Curve Theorem,
while a more general result encompassing this one is the Kuratowski Reduction Theorem. The utility graph 
is the graph showing the relationships described above. It is identical to the Thomsen Graph and, in the more
formal parlance of Graph Theory, is known as the Complete Bipartite Graph 
.
See also Complete Bipartite Graph, Kuratowski Reduction Theorem, Planar Graph, Thomsen Graph
References
Chartrand, G. ``The Three Houses and Three Utilities Problem: An Introduction to Planar Graphs.'' §9.1 in
Introductory Graph Theory. New York: Dover, pp. 191-202, 1985.
Ore, Ø. Graphs and Their Uses. New York: Random House, pp. 14-17, 1963.
Pappas, T. ``Wood, Water, Grain Problem.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 175 and 233, 1989.