|
|
|
The ultraspherical polynomials are solutions
![]() to the Ultraspherical Differential Equation for
Integer
to the Ultraspherical Differential Equation for
Integer ![]() and
and ![]() . They are generalizations of Legendre Polynomials to
. They are generalizations of Legendre Polynomials to
![]() -D space and are proportional to (or, depending on the normalization, equal to) the Gegenbauer
Polynomials
-D space and are proportional to (or, depending on the normalization, equal to) the Gegenbauer
Polynomials
![]() , denoted in Mathematica
, denoted in Mathematica
![]() (Wolfram Research, Champaign,
IL) GegenbauerC[n,lambda,x]. The ultraspherical polynomials are also Jacobi Polynomials with
(Wolfram Research, Champaign,
IL) GegenbauerC[n,lambda,x]. The ultraspherical polynomials are also Jacobi Polynomials with
![]() . They are given by the Generating Function
. They are given by the Generating Function
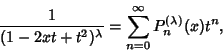 |
(1) |
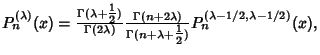
|
|
|
|
(2) |
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
In terms of the Hypergeometric Functions,
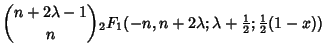 |
(7) | ||
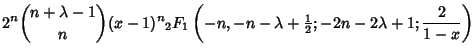 |
(8) | ||
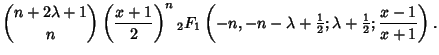 |
(9) |
| (10) |
Derivative identities include
|
|
(11) |
|
|
|
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
A Recurrence Relation is
| (19) |
Special double-![]() Formulas also exist
Formulas also exist
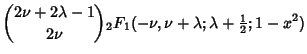 |
|||
| (20) | |||
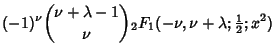 |
|||
| (21) | |||
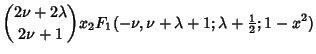 |
|||
| (22) | |||
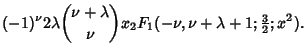 |
|||
| (23) |
Special values are given in the following table.
| Special Polynomial | |
|
|
Legendre Polynomial |
| 1 | Chebyshev Polynomial of the Second Kind |
Koschmieder (1920) gives representations in terms of Elliptic Functions for ![]() and
and ![]() .
.
See also Birthday Problem, Chebyshev Polynomial of the Second Kind, Elliptic Function, Hypergeometric Function, Jacobi Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 643, 1985.
Iyanaga, S. and Kawada, Y. (Eds.). ``Gegenbauer Polynomials (Gegenbauer Functions).'' Appendix A, Table 20.I in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1477-1478, 1980.
Koschmieder, L. ``Über besondere Jacobische Polynome.'' Math. Zeitschrift 8, 123-137, 1920.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 547-549 and 600-604, 1953.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
|
|
|
© 1996-9 Eric W. Weisstein