Triangular Symmetry Group

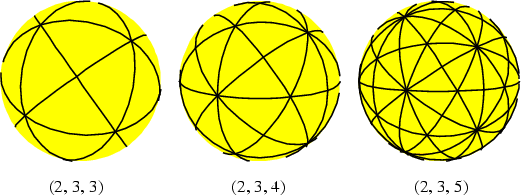
Given a Triangle with angles ($\pi/p$, $\pi/q$, $\pi/r$), the resulting symmetry Group is called a $(p,q,r)$ triangle group (also known as a Spherical Tessellation). In 3-D, such Groups must satisfy

$${1\over p}+{1\over q}+{1\over r}>1,$$

and so the only solutions are $(2,2,n)$, $(2,3,3)$, $(2,3,4)$, and $(2,3,5)$ (Ball and Coxeter 1987). The group $(2,3,6)$ gives rise to the semiregular planar Tessellations of types 1, 2, 5, and 7. The group $(2, 3, 7)$ gives hyperbolic tessellations.

See also Geodesic Dome

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 155-161, 1987.

Coxeter, H. S. M. ``The Partition of a Sphere According to the Icosahedral Group.'' Scripta Math 4, 156-157, 1936.

Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973.

Kraitchik, M. ``A Mosaic on the Sphere.'' §7.3 in Mathematical Recreations. New York: W. W. Norton, pp. 208-209, 1942.