|
|
|
A matrix for a round-robin tournament involving ![]() players competing in
players competing in ![]() matches (no ties allowed)
having entries
matches (no ties allowed)
having entries
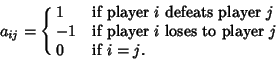
The tournament matrix for ![]() players has zero Determinant Iff
players has zero Determinant Iff ![]() is Odd (McCarthy and Benjamin 1996).
The dimension of the Nullspace of an
is Odd (McCarthy and Benjamin 1996).
The dimension of the Nullspace of an ![]() -player tournament matrix is
-player tournament matrix is
References
McCarthy, C. A. and Benjamin, A. T. ``Determinants of the Tournaments.'' Math. Mag. 69, 133-135, 1996.
Michael, T. S. ``The Ranks of Tournament Matrices.'' Amer. Math. Monthly 102, 637-639, 1995.