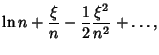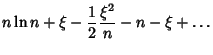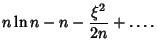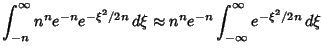Stirling's approximation gives an approximate value for the Factorial function 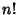 or the Gamma
Function
or the Gamma
Function 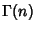 for
for 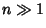 . The approximation can most simply be derived for
. The approximation can most simply be derived for 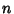 an Integer by approximating the
sum over the terms of the Factorial with an Integral, so that
an Integer by approximating the
sum over the terms of the Factorial with an Integral, so that
The equation can also be derived using the integral definition of the Factorial,
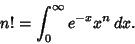 |
(2) |
Note that the derivative of the Logarithm of the integrand can be written
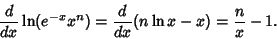 |
(3) |
The integrand is sharply peaked with the contribution important only near 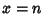 . Therefore, let
. Therefore, let 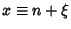 where
where
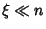 , and write
, and write
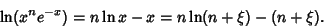 |
(4) |
Now,
so
Taking the Exponential of each side then gives
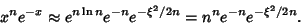 |
(7) |
Plugging into the integral expression for 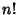 then gives
then gives
Evaluating the integral gives
Taking the Logarithm of both sides then gives
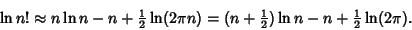 |
(11) |
This is Stirling's Series with only the first term retained and, for large 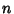 , it reduces to
Stirling's approximation
, it reduces to
Stirling's approximation
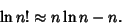 |
(12) |
Gosper notes that a better approximation to 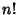 (i.e., one which approximates the terms in Stirling's Series
instead of truncating them) is given by
(i.e., one which approximates the terms in Stirling's Series
instead of truncating them) is given by
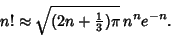 |
(13) |
This also gives a much closer approximation to the Factorial of 0, 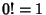 , yielding
, yielding
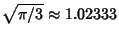 instead of 0 obtained with the conventional Stirling approximation.
instead of 0 obtained with the conventional Stirling approximation.
See also Stirling's Series
© 1996-9 Eric W. Weisstein
1999-05-26
![]() or the Gamma
Function
or the Gamma
Function ![]() for
for ![]() . The approximation can most simply be derived for
. The approximation can most simply be derived for ![]() an Integer by approximating the
sum over the terms of the Factorial with an Integral, so that
an Integer by approximating the
sum over the terms of the Factorial with an Integral, so that
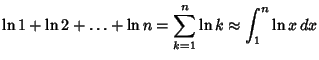
![$\displaystyle \ln\left[{n\left({1+{\xi\over n}}\right)}\right]= \ln n+\ln\left({1+{\xi\over n}}\right)$](s3_903.gif)