|
|
|
The Tangent Indicatrix of a Curve of Constant Precession is a spherical helix. The equation of a
spherical helix on a Sphere with Radius ![]() making an Angle
making an Angle ![]() with the
with the ![]() -axis is
-axis is
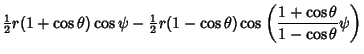 |
(1) | ||
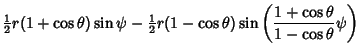 |
(2) | ||
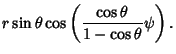 |
(3) |
| (4) | |||
| (5) |
See also Helix, Loxodrome, Spherical Spiral
References
Scofield, P. D. ``Curves of Constant Precession.'' Amer. Math. Monthly 102, 531-537, 1995.