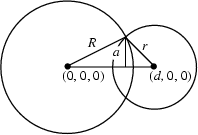
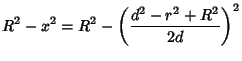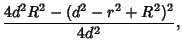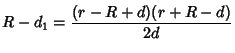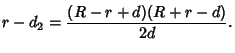Let two spheres of Radii 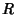 and
and 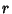 be located along the x-Axis centered at
be located along the x-Axis centered at 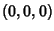 and
and
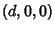 , respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.
The equations of the two Spheres are
, respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.
The equations of the two Spheres are
Combining (1) and (2) gives
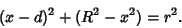 |
(3) |
Multiplying through and rearranging give
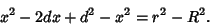 |
(4) |
Solving for 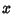 gives
gives
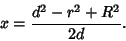 |
(5) |
The intersection of the Spheres is therefore a curve lying in a Plane parallel to the 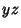 -plane at a
single
-plane at a
single 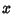 -coordinate. Plugging this back into (1) gives
-coordinate. Plugging this back into (1) gives
which is a Circle with Radius
The Volume of the 3-D Lens common to the two spheres can be found by adding the two Spherical
Caps. The distances from the Spheres' centers to the bases of the caps are
so the heights of the caps are
The Volume of a Spherical Cap of height 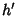 for a Sphere of Radius
for a Sphere of Radius 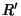 is
is
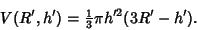 |
(12) |
Letting 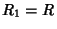 and
and 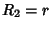 and summing the two caps gives
and summing the two caps gives
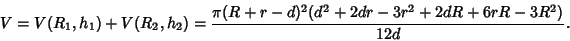 |
(13) |
This expression gives 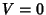 for
for 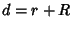 as it must. In the special case
as it must. In the special case 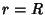 , the Volume simplifies to
, the Volume simplifies to
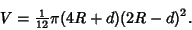 |
(14) |
See also Apple, Circle-Circle Intersection, Double Bubble, Lens,
Sphere
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() be located along the x-Axis centered at
be located along the x-Axis centered at ![]() and
and
![]() , respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.
The equations of the two Spheres are
, respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.
The equations of the two Spheres are