Smarandache-Kurepa Function

Given the sum-of-factorials function

$$\Sigma(n)=\sum_{k=1}^n k!,$$

$\mathop{\rm SK}(p)$ for $p$ Prime is the smallest integer $n$ such that $p\vert 1+\Sigma(n-1)$. The first few known values of $\mathop{\rm SK}(p)$ are 2, 4, 6, 6, 5, 7, 7, 12, 22, 16, 55, 54, 42, 24, ... for $p=2$, 5, 7, 11, 17, 19, 23, 31, 37, 41, 61, 71, 73, 89, .... The values for $p=3$, 13, 29, 43, 47, 53, 67, 79, 83, ..., if they are finite, must be very large (e.g., $\mathop{\rm SK}(3)>100,000$).

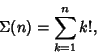
See also Pseudosmarandache Function, Smarandache Ceil Function, Smarandache Function, Smarandache-Wagstaff Function, Smarandache Function

References

Ashbacher, C. ``Some Properties of the Smarandache-Kurepa and Smarandache-Wagstaff Functions.'' Math. Informatics Quart. 7, 114-116, 1997.

Mudge, M. ``Introducing the Smarandache-Kurepa and Smarandache-Wagstaff Functions.'' Smarandache Notions J. 7, 52-53, 1996.

Mudge, M. ``Introducing the Smarandache-Kurepa and Smarandache-Wagstaff Functions.'' Abstracts of Papers Presented to the Amer. Math. Soc. 17, 583, 1996.