Smarandache-Wagstaff Function

Given the sum-of-Factorials function

$$\Sigma(n)=\sum_{k=1}^n k!,$$

${\it SW}(p)$ is the smallest integer for $p$ Prime such that $\Sigma[{\it SW}(p)]$ is divisible by $p$. The first few known values are 2, 4, 5, 12, 19, 24, 32, 19, 20, 20, 20, 7, 57, 6, ... for $p=3$, 11, 17, 23, 29, 37, 41, 43, 53, 67, 73, 79, 97, .... The values for 5, 7, 13, 31, ..., if they are finite, must be very large.

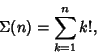
See also Factorial, Smarandache Function

References

Ashbacher, C. ``Some Properties of the Smarandache-Kurepa and Smarandache-Wagstaff Functions.'' Math. Informatics Quart. 7, 114-116, 1997.

``Functions in Number Theory.'' http://www.gallup.unm.edu/~smarandache/FUNCT1.TXT.

Mudge, M. ``Introducing the Smarandache-Kurepa and Smarandache-Wagstaff Functions.'' Smarandache Notions J. 7, 52-53, 1996.

Mudge, M. ``Introducing the Smarandache-Kurepa and Smarandache-Wagstaff Functions.'' Abstracts of Papers Presented to the Amer. Math. Soc. 17, 583, 1996.