|
|
|
A method for finding Recurrence Relations for hypergeometric polynomials directly from the
series expansions of the polynomials. The method is effective and easily implemented, but usually slower than
Zeilberger's Algorithm. Given a sum
![]() , the method operates by finding a recurrence of the form
, the method operates by finding a recurrence of the form
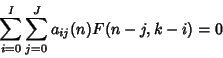
See also Generalized Hypergeometric Function, Gosper's Algorithm, Hypergeometric Identity, Hypergeometric Series, Zeilberger's Algorithm
References
Fasenmyer, Sister M. C. Some Generalized Hypergeometric Polynomials. Ph.D. thesis. University of Michigan, Nov. 1945.
Fasenmyer, Sister M. C. ``Some Generalized Hypergeometric Polynomials.'' Bull. Amer. Math. Soc. 53, 806-812, 1947.
Fasenmyer, Sister M. C. ``A Note on Pure Recurrence Relations.'' Amer. Math. Monthly 56, 14-17, 1949.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. ``Sister Celine's Method.'' Ch. 4 in A=B.
Wellesley, MA: A. K. Peters, pp. 55-72, 1996.
Rainville, E. D. Chs. 14 and 18 in Special Functions. New York: Chelsea, 1971.
Verbaten, P. ``The Automatic Construction of Pure Recurrence Relations.'' Proc. EUROSAM '74, ACM-SIGSAM Bull. 8, 96-98,
1974.
Wilf, H. S. and Zeilberger, D. ``An Algorithmic Proof Theory for Hypergeometric (Ordinary and ``
![]() '') Multisum/Integral Identities.''
Invent. Math. 108, 575-633, 1992.
'') Multisum/Integral Identities.''
Invent. Math. 108, 575-633, 1992.
|
|
|
© 1996-9 Eric W. Weisstein