Let a sequence be defined by
Also define the associated Polynomial
and let 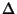 be its discriminant. The Perrin Sequence is a special case corresponding to
be its discriminant. The Perrin Sequence is a special case corresponding to 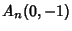 . The
signature mod
. The
signature mod 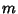 of an Integer
of an Integer 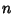 with respect to the sequence
with respect to the sequence 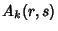 is then defined as the 6-tuple (
is then defined as the 6-tuple (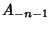 ,
,
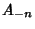 ,
, 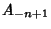 ,
, 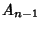 ,
, 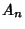 ,
, 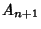 ) (mod
) (mod 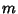 ).
).
- 1. An Integer
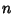 has an S-signature if its signature (mod
has an S-signature if its signature (mod 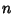 ) is (
) is (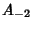 ,
, 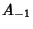 ,
, 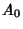 ,
, 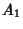 ,
, 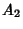 ).
).
- 2. An Integer
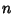 has a Q-signature if its signature (mod
has a Q-signature if its signature (mod 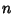 ) is Congruent to (
) is Congruent to (
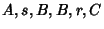 )
where, for some Integer
)
where, for some Integer 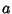 with
with
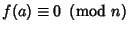 ,
,
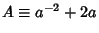 ,
,
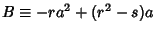 ,
and
,
and
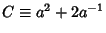 .
.
- 3. An Integer
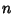 has an I-signature if its signature (mod
has an I-signature if its signature (mod 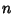 ) is Congruent to
(
) is Congruent to
(
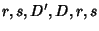 ), where
), where
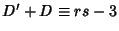 and
and
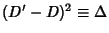 .
.
See also Perrin Pseudoprime
References
Adams, W. and Shanks, D. ``Strong Primality Tests that Are Not Sufficient.'' Math. Comput. 39, 255-300, 1982.
Grantham, J. ``Frobenius Pseudoprimes.''
http://www.clark.net/pub/grantham/pseudo/pseudo1.ps.
© 1996-9 Eric W. Weisstein
1999-05-26