The Schröder-Bernstein theorem for numbers states that if
then 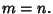 For Sets, the theorem states that if there are Injections of the Set
For Sets, the theorem states that if there are Injections of the Set
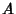 into the Set
into the Set 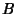 and of
and of 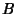 into
into 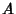 , then there is a Bijective correspondence between
, then there is a Bijective correspondence between 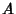 and
and
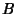 (i.e., they are Equipollent).
(i.e., they are Equipollent).
See also Bijection, Equipollent, Injection
© 1996-9 Eric W. Weisstein
1999-05-26