|
|
|
Consider a game in which a player bets on whether a given Toss of a Coin will turn up heads
or tails. If he bets $1 that heads will turn up on the first throw, $2 that heads will turn up on the second throw (if
it did not turn up on the first), $4 that heads will turn up on the third throw, etc., his expected payoff is
The paradox arises as a result of muddling the distinction between the amount of the final payoff and the net amount won in
the game. It is misleading to consider the payoff without taking into account the amount lost on previous bets, as can be
shown as follows. At the time the player first wins (say, on the ![]() th toss), he will have lost
th toss), he will have lost
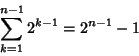
In fact, by noting that the probability of winning on the ![]() th toss is
th toss is ![]() , it can be seen that the probability
distribution for the number of tosses needed to win is simply a Geometric Distribution with
, it can be seen that the probability
distribution for the number of tosses needed to win is simply a Geometric Distribution with ![]() .
.
See also Coin Tossing, Gambler's Ruin, Geometric Distribution, Martingale
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, pp. 44-45, 1987.
Gardner, M. The Scientific American Book of Mathematical Puzzles & Diversions. New York: Simon and
Schuster, pp. 51-52, 1959.
Kamke, E. Einführung in die Wahrscheinlichkeitstheorie. Leipzig, Germany, pp. 82-89, 1932.
Keynes, J. M. K. ``The Application of Probability to Conduct.'' In
The World of Mathematics, Vol. 2 (Ed. K. Newman). Redmond, WA: Microsoft Press, 1988.
Kraitchik, M. ``The Saint Petersburg Paradox.'' §6.18 in Mathematical Recreations. New York: W. W. Norton,
pp. 138-139, 1942.
Todhunter, I. §391 in History of the Mathematical Theory of Probability. New York: Chelsea, p. 221, 1949.
|
|
|
© 1996-9 Eric W. Weisstein