|
|
|
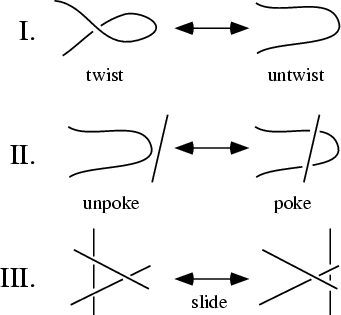
In the 1930s, Reidemeister first rigorously proved that Knots exist which are distinct from the Unknot. He did this by showing that all Knot deformations can be reduced to a sequence of three types of ``moves,'' called the (I) Twist Move, (II) Poke Move, and (III) Slide Move.
Reidemeister's Theorem guarantees that moves I, II, and III correspond to Ambient Isotopy (moves II and III alone correspond to Regular Isotopy). He then defined the concept of Colorability, which is invariant under Reidemeister moves.
See also Ambient Isotopy, Colorable, Markov Moves, Regular Isotopy, Unknot