Color each segment of a Knot Diagram using one of three colors. If
- 1. at any crossing, either the colors are all different or all the same, and
- 2. at least two colors are used,
then a Knot is said to be colorable (or more specifically, Three-Colorable). Colorability is invariant under
Reidemeister Moves, and can be generalized. For instance, for five colors 0, 1, 2, 3, and 4, a Knot is
five-colorable if
- 1. at any crossing, three segments meet. If the overpass is numbered
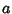 and the two underpasses
and the two underpasses 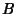 and
and 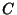 , then
, then
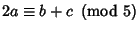 , and
, and
- 2. at least two colors are used.
Colorability cannot alway distinguish Handedness. For instance, three-colorability can distinguish the mirror
images of the Trefoil Knot but not the Figure-of-Eight Knot. Five-colorability, on the other hand,
distinguishes the Mirror Images of the Figure-of-Eight Knot but not the Trefoil Knot.
See also Coloring
© 1996-9 Eric W. Weisstein
1999-05-26