If 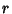 is any number and
is any number and 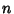 is any Integer, then there is a Rational Number
is any Integer, then there is a Rational Number 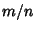 for which
for which
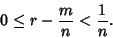 |
(1) |
If 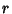 is Irrational and
is Irrational and 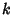 is any Whole Number, there is a Fraction
is any Whole Number, there is a Fraction 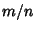 with
with
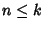 and for which
and for which
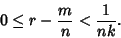 |
(2) |
Furthermore, there are an infinite number of Fractions 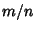 for which
for which
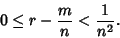 |
(3) |
Hurwitz has shown that for an Irrational Number 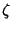
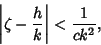 |
(4) |
there are infinitely Rational Numbers 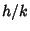 if
if
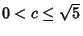 , but if
, but if 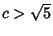 , there
are some
, there
are some 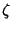 for which this approximation holds for only finitely many
for which this approximation holds for only finitely many 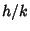 .
.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() is any number and
is any number and ![]() is any Integer, then there is a Rational Number
is any Integer, then there is a Rational Number ![]() for which
for which