|
|
|
| (1) |
| (2) |
| (3) |
Given two samples with sizes ![]() and
and ![]() and ranges
and ranges ![]() and
and ![]() , let
, let
![]() . Then
. Then
![\begin{displaymath}
D(u)=\cases{
{m(m-1)n(n-1)\over (m+n)(m+n-1)(m+n-2)}[(m+n)u...
...+n-2)u^{-n-1}]\hfill\cr
\hfill {\rm for\ } 1\leq u<\infty.\cr}
\end{displaymath}](r_667.gif) |
(4) |
| (5) |
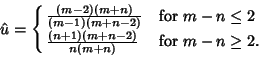 |
(6) |
References
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 213-214, 1962.