|
|
|
The q-Analog of the Binomial Theorem
|
|
|
|
|
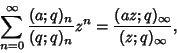
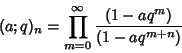
See also Binomial Series, Binomial Theorem, Cauchy Binomial Theorem, Heine Hypergeometric Series, Ramanujan Psi Sum
References
Andrews, G. E.
Heine, E. ``Untersuchungen über die Reihe
![]() -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., p. 10, 1986.
-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., p. 10, 1986.
![]() .'' J. reine angew. Math. 34, 285-328, 1847.
.'' J. reine angew. Math. 34, 285-328, 1847.