|
|
|
The Wave Equation in Prolate Spheroidal Coordinates is
|
|
|
|
|
(1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
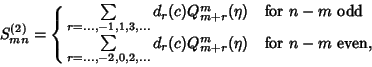 |
(8) |
| (9) |
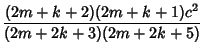 |
(10) | ||
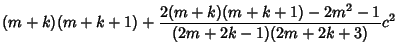 |
(11) | ||
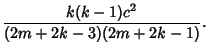 |
(12) |
Various normalization schemes are used for the ![]() s (Abramowitz and Stegun 1972, p. 758). Meixner and Schäfke (1954) use
s (Abramowitz and Stegun 1972, p. 758). Meixner and Schäfke (1954) use
| (13) |
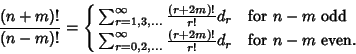 |
(14) |
| (15) |
See also Oblate Spheroidal Wave Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Spheroidal Wave Functions.'' Ch. 21 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 751-759, 1972.
Flammer, C. Spheroidal Wave Functions. Stanford, CA: Stanford University Press, 1957.
Meixner, J. and Schäfke, F. W. Mathieusche Funktionen und Sphäroidfunktionen. Berlin: Springer-Verlag, 1954.
Stratton, J. A.; Morse, P. M.; Chu, L. J.; Little, J. D. C.; and Corbató, F. J. Spheroidal Wave Functions.
New York: Wiley, 1956.
|
|
|
© 1996-9 Eric W. Weisstein