A general Quintic Equation
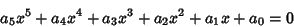 |
(1) |
can be reduced to one of the form
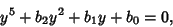 |
(2) |
called the principal quintic form.
Newton's Relations for the Roots 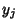 in terms of the
in terms of the 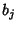 s is a linear system in the
s is a linear system in the 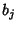 , and solving for
the
, and solving for
the 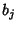 s expresses them in terms of the Power sums
s expresses them in terms of the Power sums 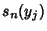 . These Power sums can be expressed in terms
of the
. These Power sums can be expressed in terms
of the 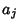 s, so the
s, so the 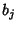 s can be expressed in terms of the
s can be expressed in terms of the 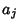 s. For a quintic to have no quartic or cubic term, the
sums of the Roots and the sums of the Squares of the Roots vanish, so
s. For a quintic to have no quartic or cubic term, the
sums of the Roots and the sums of the Squares of the Roots vanish, so
Assume that the Roots 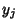 of the new quintic are related to the Roots
of the new quintic are related to the Roots 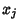 of the original quintic by
of the original quintic by
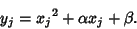 |
(5) |
Substituting this into (1) then yields two equations for 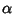 and
and 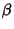 which can be multiplied out, simplified by using
Newton's Relations for the Power sums in the
which can be multiplied out, simplified by using
Newton's Relations for the Power sums in the 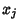 , and finally solved. Therefore,
, and finally solved. Therefore, 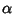 and
and 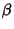 can be
expressed using Radicals in terms of the Coefficients
can be
expressed using Radicals in terms of the Coefficients 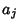 . Again by substitution
into (4), we can calculate
. Again by substitution
into (4), we can calculate 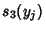 ,
, 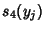 and
and 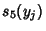 in terms of
in terms of 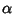 and
and 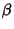 and the
and the 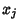 . By the
previous solution for
. By the
previous solution for 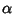 and
and 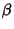 and again by using Newton's Relations for the Power sums in the
and again by using Newton's Relations for the Power sums in the
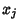 , we can ultimately express these Power sums in terms of the
, we can ultimately express these Power sums in terms of the 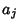 .
.
See also Bring Quintic Form, Newton's Relations, Quintic Equation
© 1996-9 Eric W. Weisstein
1999-05-26
![]() in terms of the
in terms of the ![]() s is a linear system in the
s is a linear system in the ![]() , and solving for
the
, and solving for
the ![]() s expresses them in terms of the Power sums
s expresses them in terms of the Power sums ![]() . These Power sums can be expressed in terms
of the
. These Power sums can be expressed in terms
of the ![]() s, so the
s, so the ![]() s can be expressed in terms of the
s can be expressed in terms of the ![]() s. For a quintic to have no quartic or cubic term, the
sums of the Roots and the sums of the Squares of the Roots vanish, so
s. For a quintic to have no quartic or cubic term, the
sums of the Roots and the sums of the Squares of the Roots vanish, so