Petrie Polygon

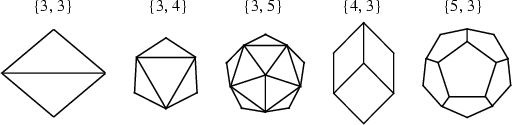
$\begin{figure}\begin{center}\BoxedEPSF{Petrie_Polygons.epsf scaled 850}\end{center}\end{figure}$

A skew Polygon such that every two consecutive sides (but no three) belong to a face of a regular Polyhedron. Every finite Polyhedron can be orthogonally projected onto a plane in such a way that one Petrie polygon becomes a Regular Polygon with the remainder of the projection interior to it. The Petrie polygon of the Polyhedron $\{p, q\}$ has sides, where

$\begin{displaymath} \cos^2\left({\pi\over h}\right)=\cos^2\left({\pi\over p}\right)+\cos^2\left({\pi\over q}\right). \end{displaymath}$

The Petrie polygons shown above correspond to the Platonic Solids.

See also Platonic Solid, Regular Polygon

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 135, 1987.

Coxeter, H. S. M. ``Petrie Polygons.'' §2.6 in Regular Polytopes, 3rd ed. New York: Dover, pp.24-25, 1973.