Parallelogram

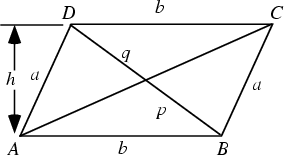
A Quadrilateral with opposite sides parallel (and therefore opposite angles equal). A quadrilateral with equal sides is called a Rhombus, and a parallelogram whose Angles are all Right Angles is called a Rectangle.

A parallelogram of base $b$ and height $h$ has Area

$$A = bh = ab\sin A=ab\sin B.$$ (1)

The height of a parallelogram is

$$h=a\sin A=a\sin B,$$ (2)

and the Diagonals are

$$p = \sqrt{a^2+b^2-2ab\cos A}$$ (3)

$$q = \sqrt{a^2+b^2-2ab\cos B}$$ (4)

$$= \sqrt{a^2+b^2+2ab\cos A}$$ (5)

(Beyer 1987).

The Area of the parallelogram with sides formed by the Vectors $(a,c)$ and $(b,d)$ is

$$A={\rm det}\left({\left[{\matrix{a & b\cr c & d\cr}}\right]}\right)= \vert ad-bc\vert.$$ (6)

Given a parallelogram $P$ with area $A(P)$ and linear transformation $T$, the Area of $T(P)$ is

$$A(T(P)) = \left\vert\matrix{a & b\cr c & d\cr}\right\vert A(P).$$ (7)

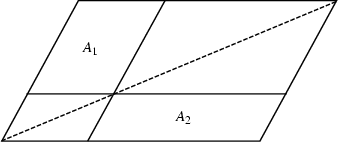
As shown by Euclid, if lines parallel to the sides are drawn through any point on a diagonal of a parallelogram, then the parallelograms not containing segments of that diagonal are equal in Area (and conversely), so in the above figure, $A_1=A_2$ (Johnson 1929).

See also Diamond, Lozenge, Parallelogram Illusion, Rectangle, Rhombus, Varignon Parallelogram, Wittenbauer's Parallelogram

References

Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 123, 1987.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, p. 61, 1929.