|
|
|
A Geodesic on a Paraboloid has differential parameters defined by
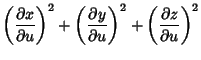 |
|||
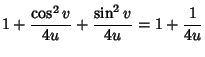 |
(1) | ||
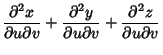 |
|||
| (2) | |||
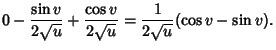 |
(3) |
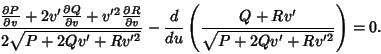 |
(4) |
| (5) |
See also Geodesic
References
Weinstock, R. Calculus of Variations, with Applications to Physics and Engineering.
New York: Dover, p. 45, 1974.