|
|
|
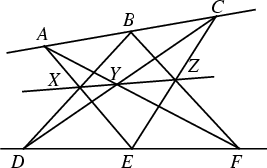
If ![]() ,
, ![]() , and
, and ![]() are three points on one Line,
are three points on one Line, ![]() ,
, ![]() , and
, and ![]() are three points on another Line, and
are three points on another Line, and ![]() meets
meets ![]() at
at ![]() ,
, ![]() meets
meets ![]() at
at ![]() , and
, and ![]() meets
meets ![]() at
at ![]() , then the three points
, then the three points ![]() ,
, ![]() , and
, and ![]() are
Collinear. Pappus's hexagon theorem dual to Desargues' Theorem according to the Duality Principle of
Projective Geometry.
are
Collinear. Pappus's hexagon theorem dual to Desargues' Theorem according to the Duality Principle of
Projective Geometry.
See also Cayley-Bacharach Theorem, Desargues' Theorem, Duality Principle, Pascal's Theorem, Projective Geometry
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 73-74, 1967.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 92-94, 1990.
Pappas, T. ``Pappus' Theorem & the Nine Coin Puzzle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra,
p. 163, 1989.