|
|
|
The center of any Sphere which has a contact of (at least) first-order with a curve ![]() at a point
at a point ![]() lies
in the normal plane to
lies
in the normal plane to ![]() at
at ![]() . The center of any Sphere which has a contact of (at least) second-order with
. The center of any Sphere which has a contact of (at least) second-order with ![]() at point
at point ![]() , where the Curvature
, where the Curvature ![]() , lies on the polar axis of
, lies on the polar axis of ![]() corresponding to
corresponding to ![]() . All these
Spheres intersect the Osculating Plane of
. All these
Spheres intersect the Osculating Plane of ![]() at
at ![]() along a circle of curvature at
along a circle of curvature at ![]() .
The osculating sphere has center
.
The osculating sphere has center
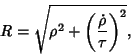
See also Curvature, Osculating Plane, Radius of Curvature, Sphere, Torsion (Differential Geometry)
References
Kreyszig, E. Differential Geometry. New York: Dover, pp. 54-55, 1991.