The Plane spanned by the three points 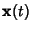 ,
,
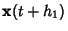 , and
, and
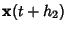 on a curve as
on a curve as 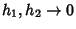 . Let
. Let 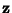 be a point on the osculating plane, then
be a point on the osculating plane, then
where
![$[{\bf A},{\bf B},{\bf C}]$](o_1073.gif) denotes the Scalar Triple Product. The osculating plane passes through the tangent.
The intersection of the osculating plane with the Normal Plane is known as the Principal Normal Vector. The
Vectors
denotes the Scalar Triple Product. The osculating plane passes through the tangent.
The intersection of the osculating plane with the Normal Plane is known as the Principal Normal Vector. The
Vectors 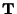 and
and 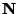 (Tangent Vector and Normal Vector) span the osculating plane.
(Tangent Vector and Normal Vector) span the osculating plane.
See also Normal Vector, Osculating Sphere, Scalar Triple Product, Tangent Vector
© 1996-9 Eric W. Weisstein
1999-05-26
![]() ,
,
![]() , and
, and
![]() on a curve as
on a curve as ![]() . Let
. Let ![]() be a point on the osculating plane, then
be a point on the osculating plane, then