A nonuniform rational B-Spline curve defined by
where 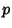 is the order,
is the order, 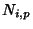 are the B-Spline basis functions,
are the B-Spline basis functions, 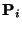 are control points, and
the weight
are control points, and
the weight 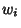 of
of 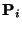 is the last ordinate of the homogeneous point
is the last ordinate of the homogeneous point 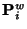 . These curves are
closed under perspective transformations and can represent Conic Sections exactly.
. These curves are
closed under perspective transformations and can represent Conic Sections exactly.
See also B-Spline, Bézier Curve, NURBS Surface
References
Piegl, L. and Tiller, W. The NURBS Book, 2nd ed New York: Springer-Verlag, 1997.
© 1996-9 Eric W. Weisstein
1999-05-25