|
|
|
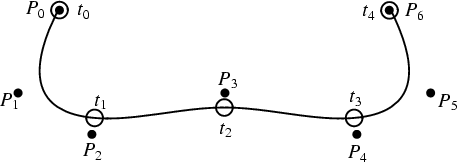
A generalization of the Bézier Curve. Let a vector known as the Knot Vector be
defined
| (1) |
| (2) |
Define the basis functions as
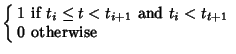 |
(3) | ||
| (4) |
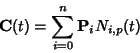 |
(5) |
The degree of a B-spline is independent of the number of control points, so a low order can always be maintained for
purposes of numerical stability. Also, a curve is ![]() times differentiable at a point where
times differentiable at a point where ![]() duplicate knot
values occur. The knot values determine the extent of the control of the control points.
duplicate knot
values occur. The knot values determine the extent of the control of the control points.
See also Bézier Curve, NURBS Curve