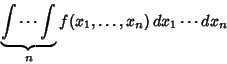Multiple Integral

A repeated integral over 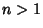$n>1$ variables

$$\underbrace{\int\cdots\int}_n f(x_1, \ldots, x_n)\,dx_1\cdots dx_n$$

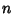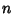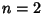is called a multiple integral. An $n$th order integral corresponds, in general, to an $n$-D Volume (Content), with $n=2$ corresponding to an Area. In an indefinite multiple integral, the order in which the integrals are carried out can be varied at will; for definite multiple integrals, care must be taken to correctly transform the limits if the order is changed.

See also Integral, Monte Carlo Integration

References

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Multidimensional Integrals.'' §4.6 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 155-158, 1992.