|
|
|
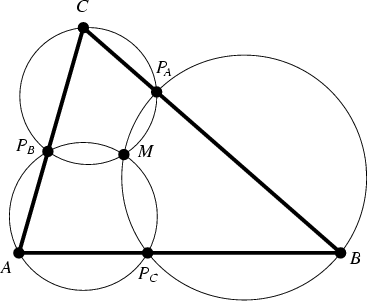
For a Triangle ![]() and three points
and three points ![]() ,
, ![]() , and
, and ![]() , one on each of its sides, the three Miquel circles
are the circles passing through each Vertex and its neighboring side points (i.e.,
, one on each of its sides, the three Miquel circles
are the circles passing through each Vertex and its neighboring side points (i.e., ![]() ,
,
![]() , and
, and ![]() ). According to Miquel's Theorem, the Miquel circles are Concurrent in a point
). According to Miquel's Theorem, the Miquel circles are Concurrent in a point ![]() known as
the Miquel Point. Similarly, there are
known as
the Miquel Point. Similarly, there are ![]() Miquel circles for
Miquel circles for ![]() lines taken
lines taken ![]() at a time.
at a time.
See also Miquel Point, Miquel's Theorem, Miquel Triangle