|
|
|
The sequence produced by starting with ![]() and applying the Greedy Algorithm in the following way: for each
and applying the Greedy Algorithm in the following way: for each
![]() , let
, let ![]() be the least Integer exceeding
be the least Integer exceeding ![]() for which
for which ![]() are all distinct, with
are all distinct, with ![]() .
This procedure generates the sequence 1, 2, 4, 8, 13, 21, 31, 45, 66, 81, 97, 123, 148, 182, 204, 252, 290, ...
(Sloane's A005282). The Reciprocal sum of the sequence,
.
This procedure generates the sequence 1, 2, 4, 8, 13, 21, 31, 45, 66, 81, 97, 123, 148, 182, 204, 252, 290, ...
(Sloane's A005282). The Reciprocal sum of the sequence,
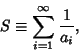
See also A-Sequence, B2-Sequence
References
Guy, R. K. ``
Sloane, N. J. A. Sequence
A005282/M1094
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() -Sequences.'' §E28 in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 228-229, 1994.
-Sequences.'' §E28 in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 228-229, 1994.