B2-Sequence

N.B. A detailed on-line essay by S. Finch was the starting point for this entry.

Also called a Sidon Sequence. An Infinite Sequence of Positive Integers

$$1\leq b_1<b_2<b_3<\ldots$$ (1)

such that all pairwise sums

$$b_i+b_j$$ (2)

for $i\leq j$ are distinct (Guy 1994). An example is 1, 2, 4, 8, 13, 21, 31, 45, 66, 81, ... (Sloane's A005282).

Zhang (1993, 1994) showed that

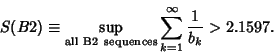$$S(B2)\equiv \sup_{\rm all\ B2\ sequences} \sum_{k=1}^\infty {1\over b_k}>2.1597.$$ (3)

The definition can be extended to $B_n$-sequences (Guy 1994).

See also A-Sequence, Mian-Chowla Sequence

References

Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/erdos/erdos.html

Guy, R. K. ``Packing Sums of Pairs,'' ``Three-Subsets with Distinct Sums,'' and ``$B_2$-Sequences,'' and $B_2$-Sequences Formed by the Greedy Algorithm.'' §C9, C11, E28, and E32 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 115-118, 121-123, 228-229, and 232-233, 1994.

Sloane, N. J. A. Sequence A005282/M1094 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Zhang, Z. X. ``A B2-Sequence with Larger Reciprocal Sum.'' Math. Comput. 60, 835-839, 1993.

Zhang, Z. X. ``Finding Finite B2-Sequences with Larger $m-{a_m}^{1/2}$.'' Math. Comput. 63, 403-414, 1994.