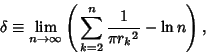Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/masser/masser.html
Gramain, F. ``Sur le théorème de Fukagawa-Gel'fond.'' Invent. Math. 63, 495-506, 1981.
Gramain, F. ``Sur le théorème de Fukagawa-Gel'fond-Gruman-Masser.'' Séminaire Delange-Pisot-Poitou
(Théorie des Nombres), 1980-1981. Boston, MA: Birkhäuser, 1982.
Gramain, F. and Weber, M. ``Computing and Arithmetic Constant Related to the Ring of Gaussian Integers.''
Math. Comput. 44, 241-245, 1985.
Gramain, F. and Weber, M. ``Computing and Arithmetic Constant Related to the Ring of Gaussian Integers.''
Math. Comput. 48, 854, 1987.
Masser, D. W. ``Sur les fonctions entières à valeurs entières.'' C. R. Acad. Sci. Paris Sér. A-B 291, A1-A4, 1980.
![]() be an Entire Function such that
be an Entire Function such that ![]() is an Integer for each Positive Integer
is an Integer for each Positive Integer ![]() .
Then Pólya (1915) showed that if
.
Then Pólya (1915) showed that if
![]() is an Entire Function with
is an Entire Function with ![]() a Gaussian Integer for each Gaussian Integer
a Gaussian Integer for each Gaussian Integer ![]() , then
Gelfond (1929) proved that there exists a constant
, then
Gelfond (1929) proved that there exists a constant ![]() such that
such that