|
|
|
The quantities obtained from cubic, hexagonal, etc., Lattice Sums, evaluated at ![]() , are called
Madelung constants. For cubic Lattice Sums, they are expressible in closed form for Even indices,
, are called
Madelung constants. For cubic Lattice Sums, they are expressible in closed form for Even indices,
| (1) | |||
| (2) |
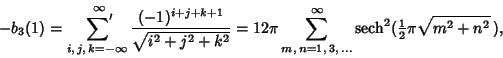 |
(3) |
For hexagonal Lattice Sum, ![]() is expressible in closed form as
is expressible in closed form as
| (4) |
See also Benson's Formula, Lattice Sum
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational
Complexity. New York: Wiley, 1987.
Buhler, J. and Wagon, S. ``Secrets of the Madelung Constant.'' Mathematica in Education and Research 5, 49-55, Spring 1996.
Crandall, R. E. and Buhler, J. P. ``Elementary Function Expansions for
Madelung Constants.'' J. Phys. Ser. A: Math. and Gen. 20, 5497-5510, 1987.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/mdlung/mdlung.html