|
|
|
Cubic lattice sums include the following:
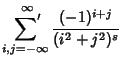 |
(1) | ||
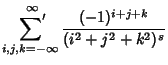 |
(2) | ||
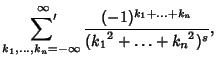 |
(3) |
| (4) | |||
| (5) | |||
| (6) |
For hexagonal sums, Borwein and Borwein (1987, p. 292) give
![\begin{displaymath}
h_2(2s)\equiv {4\over 3}\sum_{m, n=-\infty}^\infty {\sin[(n+...
...tstyle{1\over 2}}m)^2+3({\textstyle{1\over 2}}m)^2}\right]^s},
\end{displaymath}](l1_880.gif) |
(7) |
| (8) |
See also Benson's Formula, Madelung Constants
References
Borwein, D. and Borwein, J. M. ``On Some Trigonometric and Exponential Lattice Sums.'' J. Math. Anal. 188, 209-218, 1994.
Borwein, D.; Borwein, J. M.; and Shail, R. ``Analysis of Certain Lattice Sums.'' J. Math. Anal. 143, 126-137, 1989.
Borwein, D. and Borwein, J. M. ``A Note on Alternating Series in Several Dimensions.'' Amer. Math. Monthly 93, 531-539, 1986.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/mdlung/mdlung.html
Glasser, M. L. and Zucker, I. J. ``Lattice Sums.'' In Perspectives in Theoretical Chemistry: Advances and Perspectives 5,
67-139, 1980.
|
|
|
© 1996-9 Eric W. Weisstein