|
|
|
For all integers ![]() and
and ![]() ,
,
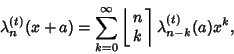
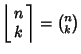 when
when
Similarly, taking ![]() and
and ![]() gives the
Negative Binomial Series. Roman (1992) gives expressions obtained for the case
gives the
Negative Binomial Series. Roman (1992) gives expressions obtained for the case ![]() and
and ![]() which are not
obtainable from the Binomial Theorem.
which are not
obtainable from the Binomial Theorem.
See also Harmonic Logarithm, Roman Coefficient
References
Roman, S. ``The Logarithmic Binomial Formula.'' Amer. Math. Monthly 99, 641-648, 1992.