|
|
|
A generalization of the Binomial Coefficient whose Notation was suggested by Knuth,
| (1) |
| (2) | |||
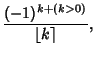 |
(3) |
| (4) |
The Roman coefficients also satisfy properties like those of the Binomial Coefficient,
| (5) |
| (6) |
| (7) |
| (8) |
See also Binomial Coefficient, Roman Factorial
References
Roman, S. ``The Logarithmic Binomial Formula.'' Amer. Math. Monthly 99, 641-648, 1992.