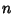 Vectors
Vectors 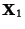 ,
, 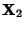 , ...,
, ..., 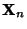 are linearly dependent Iff there
exist Scalars
are linearly dependent Iff there
exist Scalars 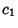 ,
, 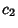 , ...,
, ..., 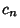 , not all zero, such that
, not all zero, such that
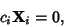 |
(1) |
where Einstein Summation is used and 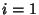 , ...,
, ..., 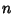 . If no such Scalars exist,
then the vectors are said to be linearly independent. In order to satisfy the Criterion for linear dependence,
. If no such Scalars exist,
then the vectors are said to be linearly independent. In order to satisfy the Criterion for linear dependence,
![\begin{displaymath}
c_1\left[{\matrix{x_{11}\cr x_{21}\cr \vdots\cr x_{n1}\cr}}\...
...}\cr}}\right]=\left[{\matrix{0\cr 0\cr \vdots\cr 0\cr}}\right]
\end{displaymath}](l2_366.gif) |
(2) |
![\begin{displaymath}
\left[{\matrix{
x_{11} & x_{12} & \cdots & x_{1n}\cr
x_{21...
...}}\right]
= \left[{\matrix{0\cr 0\cr \vdots\cr 0\cr}}\right].
\end{displaymath}](l2_367.gif) |
(3) |
In order for this Matrix equation to have a nontrivial solution, the Determinant must be 0, so the
Vectors are linearly dependent if
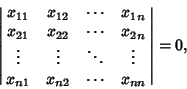 |
(4) |
and linearly independent otherwise.
Let 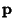 and
and 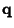 be
be 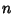 -D Vectors. Then the following three conditions are equivalent
(Gray 1993).
-D Vectors. Then the following three conditions are equivalent
(Gray 1993).
- 1.
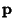 and
and 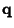 are linearly dependent.
are linearly dependent.
- 2.
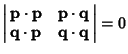 .
.
- 3. The
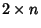 Matrix
Matrix
![$\left[{\matrix{{\bf p}\cr {\bf q}\cr}}\right]$](l2_373.gif) has rank less than two.
has rank less than two.
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 186-187, 1993.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() Vectors
Vectors ![]() ,
, ![]() , ...,
, ..., ![]() are linearly dependent Iff there
exist Scalars
are linearly dependent Iff there
exist Scalars ![]() ,
, ![]() , ...,
, ..., ![]() , not all zero, such that
, not all zero, such that
![\begin{displaymath}
c_1\left[{\matrix{x_{11}\cr x_{21}\cr \vdots\cr x_{n1}\cr}}\...
...}\cr}}\right]=\left[{\matrix{0\cr 0\cr \vdots\cr 0\cr}}\right]
\end{displaymath}](l2_366.gif)
![\begin{displaymath}
\left[{\matrix{
x_{11} & x_{12} & \cdots & x_{1n}\cr
x_{21...
...}}\right]
= \left[{\matrix{0\cr 0\cr \vdots\cr 0\cr}}\right].
\end{displaymath}](l2_367.gif)
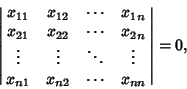
![]() and
and ![]() be
be ![]() -D Vectors. Then the following three conditions are equivalent
(Gray 1993).
-D Vectors. Then the following three conditions are equivalent
(Gray 1993).
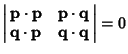 .
.