|
|
|
A generalization of the Hurwitz Zeta Function and Polylogarithm function. Many sums of reciprocal Powers
can be expressed in terms of it. It is defined by
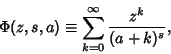 |
(1) |
The Lerch transcendent can be used to express the Dirichlet Beta Function
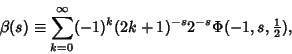 |
(2) |
| (3) |
See also Dirichlet Beta Function, Dirichlet L-Series, Fermi-Dirac Distribution, Hurwitz Zeta Function, Polylogarithm