|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() denote the partition lattice of the Set
denote the partition lattice of the Set
![]() . The Maximum element of
. The Maximum element of ![]() is
is
| (1) |
| (2) |
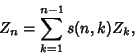 |
(3) |
| (4) |
| (5) |
References
Babai, L. and Lengyel, T. ``A Convergence Criterion for Recurrent Sequences with Application to the Partition
Lattice.'' Analysis 12, 109-119, 1992.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lngy/lngy.html
Flajolet, P. and Salvy, B. ``Hierarchal Set Partitions and Analytic Iterates of the Exponential Function.''
Unpublished manuscript, 1990.
Lengyel, T. ``On a Recurrence Involving Stirling Numbers.'' Europ. J. Comb. 5, 313-321, 1984.
Plouffe, S. ``The Lengyel Constant.''
http://www.lacim.uqam.ca/piDATA/lengyel.txt.