A Laurent polynomial with Coefficients in the Field 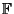 is an algebraic object
that is typically expressed in the form
is an algebraic object
that is typically expressed in the form
where the 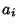 are elements of
are elements of 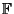 , and only finitely many of the
, and only finitely many of the 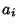 are Nonzero. A Laurent polynomial is an
algebraic object in the sense that it is treated as a Polynomial except that the indeterminant ``
are Nonzero. A Laurent polynomial is an
algebraic object in the sense that it is treated as a Polynomial except that the indeterminant ``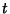 '' can also
have Negative Powers.
'' can also
have Negative Powers.
Expressed more precisely, the collection of Laurent polynomials with Coefficients in a Field
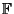 form a Ring, denoted
form a Ring, denoted
![$\Bbb{F}[t,t^{-1}]$](l1_886.gif) , with Ring operations given by componentwise addition and
multiplication according to the relation
, with Ring operations given by componentwise addition and
multiplication according to the relation
for all 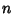 and
and 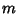 in the Integers. Formally, this is equivalent to saying that
in the Integers. Formally, this is equivalent to saying that
![$\Bbb{F}[t,t^{-1}]$](l1_886.gif) is
the Group Ring of the Integers and the Field
is
the Group Ring of the Integers and the Field 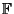 . This corresponds to
. This corresponds to ![$\Bbb{F}[t]$](l1_888.gif) (the Polynomial ring in one variable for
(the Polynomial ring in one variable for 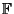 ) being the Group Ring or Monoid ring for the
Monoid of natural numbers and the Field
) being the Group Ring or Monoid ring for the
Monoid of natural numbers and the Field 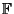 .
.
See also Polynomial
References
Lang, S. Undergraduate Algebra, 2nd ed. New York: Springer-Verlag, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is an algebraic object
that is typically expressed in the form
is an algebraic object
that is typically expressed in the form
![]() form a Ring, denoted
form a Ring, denoted
![]() , with Ring operations given by componentwise addition and
multiplication according to the relation
, with Ring operations given by componentwise addition and
multiplication according to the relation