|
|
|
A theorem outlined in 1954 by Kolmogorov which was subsequently proved in the 1960s by Arnold and Moser (Tabor 1989,
p. 105). It gives conditions under which Chaos is restricted in extent. Moser's 1962 proof was valid for
Twist Maps
| (1) | |||
| (2) |
| (3) |
Moser considered an integrable Hamiltonian function ![]() with a Torus
with a Torus ![]() and set of frequencies
and set of frequencies ![]() having an
incommensurate frequency vector
having an
incommensurate frequency vector
![]() (i.e.,
(i.e.,
![]() for all Integers
for all Integers ![]() ).
Let
).
Let ![]() be perturbed by some periodic function
be perturbed by some periodic function ![]() . The KAM theorem states that, if
. The KAM theorem states that, if ![]() is small enough, then for
almost every
is small enough, then for
almost every ![]() there exists an invariant Torus
there exists an invariant Torus ![]() of the perturbed system such that
of the perturbed system such that ![]() is ``close to''
is ``close to'' ![]() . Moreover, the Tori
. Moreover, the Tori ![]() form a set of Positive measures whose
complement has a measure which tends to zero as
form a set of Positive measures whose
complement has a measure which tends to zero as ![]() . A useful paraphrase of the KAM theorem is, ``For sufficiently
small perturbation, almost all Tori (excluding those with rational frequency vectors) are preserved.'' The
theorem thus explicitly excludes Tori with rationally related frequencies, that is,
. A useful paraphrase of the KAM theorem is, ``For sufficiently
small perturbation, almost all Tori (excluding those with rational frequency vectors) are preserved.'' The
theorem thus explicitly excludes Tori with rationally related frequencies, that is, ![]() conditions of the
form
conditions of the
form
| (4) |
| (5) |
| (6) |
The KAM theorem broke the deadlock of the small divisor problem in classical perturbation theory, and provides the starting
point for an understanding of the appearance of Chaos. For a Hamiltonian System, the Isoenergetic
Nondegeneracy condition
| (7) |
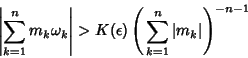 |
(8) |
See also Chaos, Hamiltonian System, Quasiperiodic Function, Torus
References
Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.
|
|
|
© 1996-9 Eric W. Weisstein